LS-DYNA引入不可压缩光滑粒子伽辽金方法ISPG,以拉格朗日方式求解纳维-斯托克斯方程。本方法旨在解决强形式拉格朗日粒子法在求解不可压缩自由表面流动时关键的数值不稳定性问题。ISPG方法提供了一种稳健和有效的方法求解精确的结果,包括流固耦合。
回流焊工艺涉及多个设计因素,这些因素能够影响熔融焊点的结果形状,如焊点体积、恢复力、表面张力、接触角、焊盘厚度和焊盘尺寸等,采用ISPG方法进行模拟时能将这些因素都考虑在内。使用基于节点云的网格重划分和节点删除与插入的算法用于处理焊料拓扑形状的变化,包括焊料桥接和焊料分离以及非常复杂的边界条件,比如尖角。仿真计算结果与理论分析结果吻合较好,表明该方法可用于SMD/NSMD焊点回流形状的预测。该研究为设计人员准确预测回流焊过程中焊点的液体形成提供了基本指导。同时,近期自适应ISPG方法在各种粘接接头和涂层问题中的粘胶流动模拟中的同样有着成功的应用案例。本文将主要介绍:
对于显式求解器来说,不可压流体计算由于受材料体积模量的限制,时间步长非常小,带来巨大的计算量,即使模拟1~2秒工况问题,也需要耗费几天甚至十几天的计算时间。而隐式算法则可以避免这类不足,其时间步长可以较大,计算效率显著提高,相对于显式在不可压缩流体计算方面有着巨大的优势。虽然ISPG方法更偏向于是一种基于粒子的伽辽金方法,但它仍然需要借助网格来积分,而流体的变形往往会非常的大,若网格的变形太大,很多问题也无法进行计算。因此LS-DYNA研发了一种新的方法:自适应网格更新ISPG方法,该方法种网格会持续不停的更新,形成非常规则的网格,从而能够实现隐式求解时更快的迭代速度及更高的效率。大变形问题中若网格不能及时更新,很可能出现不收敛等情况。
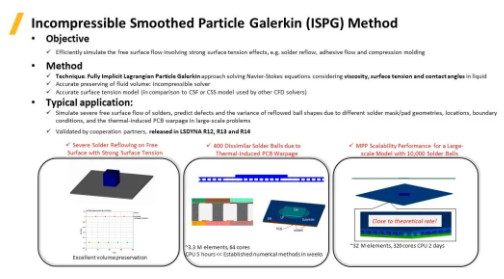
ISPG的全称为Incompressible Smoothed Particle Galerkin Method不可压缩光滑粒子伽辽金法,是完全的隐式计算方法。ISPG可有效地求解涉及强表面张力效应的自由表面流动问题,如回流焊,粘胶流动和压缩成形等。ISPG基于完全隐式拉格朗日粒子伽辽金方法求解考虑液体粘度、表面张力和接触角的Navier-Stokes方程,可精确地保持流体体积,能够精确地模拟回流焊过程中焊球形状形成的过程(考虑自由表面流、表面张力和附着力),研究回流焊工艺过程中可能出现的缺陷,如翘曲、桥接和虚焊等。
上图中左一案例为具有强表面张力的自由表面的回流焊模拟,焊球在温度影响下逐渐展现流体的性质,在接触壁面时,其表面在表面附着力的作用下扩张,形成非常大的变形。由于使用的是不可压的流体求解器,模拟过程中焊球的体积变化几乎为零,说明ISPG方法在保持体积方面表现非常优秀。中间案例为由于热膨胀引起PCB电路板翘曲中回流焊焊接的过程,在流体表面施加边界条件进行流固耦合计算,模拟过程精确预测了每个焊球的变形过程。右一案例显示了具有10,000个焊球的大型模型,该模型包含3200万单元并使用320核CPU,基于全隐式计算,计算在2天内完成,展示了LS-DYNA ISPG计算大规模模型的强大能力。
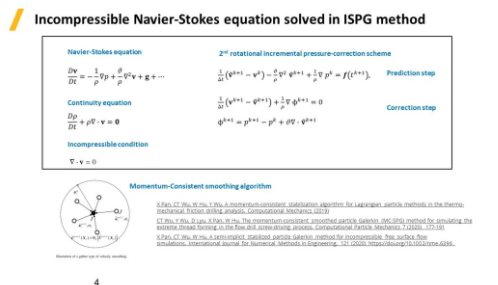
ISPG方法的基本理论。作为一种流体求解器,ISPG以拉格朗日方式求解Navier-Stokes方程,同时加入流体的连续性方程和不可压缩条件,通过动量守恒光滑算法,基于隐式求解得到相对应的压力、速度和位移。感兴趣的用户可以参考以下三篇论文:
X Pan, CT Wu, W Hu, Y Wu, A momentum-consistent stabilization algorithm for Lagrangian particle methods in the thermo-mechanical friction drilling analysis, Computational Mechanics (2019)
CT Wu, Y Wu, D Lyu, X Pan, W Hu, The momentum-consistent smoothed particle Galerkin (MC-SPG) method for simulating the extreme thread forming in the flow drill screw-driving process, Computational Particle Mechanics 7 (2020) 177-191
X Pan, CT Wu, W Hu, A semi-implicit stabilized particle Galerkin method for incompressible free surface flow simulations, International Journal for Numerical Methods in Engineering, 121 (2020) https://doi.org/10.1002/nme.6396

回流焊过程包含大量复杂的物理现象如:翘曲、自由表面流动、强表面张力、壁面粘附、热相关、流体熔合(分离)、相变等。而常规欧拉方法Eulerian在自由表面流动模拟中的困难主要表现为:
难以跟踪自由表面和界面(VOF技术,耗时);
难以处理与流体耦合的翘曲结构;
而ISPG方法是一种拉格朗日方法,颗粒随着材料变形运动,材料变形的表面即为颗粒的表面,更适合流体边界的求解以及流固耦合的模拟过程。
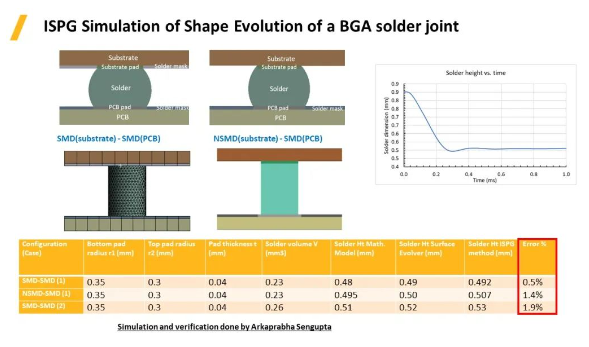
回流焊的过程通常有两种方式:SMD(Solder Mask Defined防焊限定焊垫,其基质上有一层阻焊层:防焊绿油/绿漆(Solder-Mask以及NSMD (Non-Solder Mask Defined非防焊限定焊垫,又称铜箔独立焊垫)。
如案例所示,在基板上施加重力,部件向下移动过程中焊球在表面张力作用下形成一个向上托力,焊球高度在变化过程中有一段震动后达到平衡,随后测量基板与PCB两个面之间的距离来得出焊球的高度,与理论值进行对比,根据图中表格可以看出三组数据的误差都在2%之内,体现了超高的精度值。
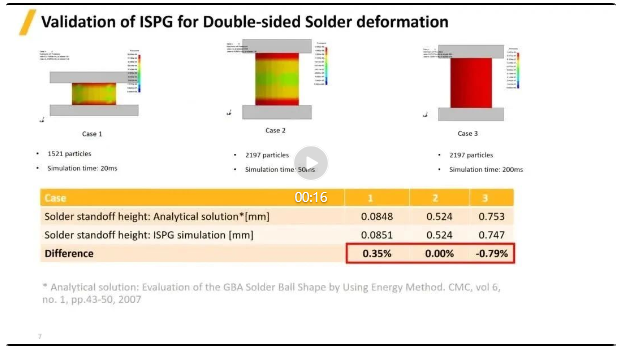
点击图片即可跳转原文观看视频
上图案例展示了另外一个验证过程,不同尺寸和重量的焊球在双层板挤压下,由于表面张力的作用形成的结果变形形状,结果表明精度非常高,误差小于1%。
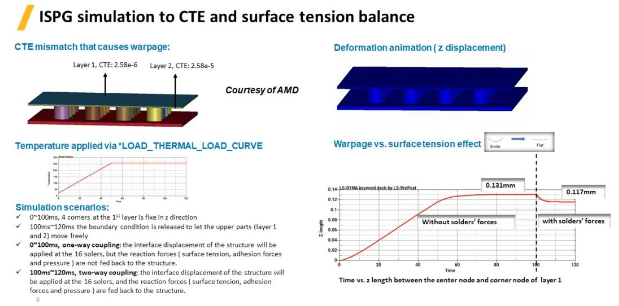
下面是一个PCB翘曲变形与焊球表面张力平衡的案例。由于不同层级电路板之间的热膨胀系数不一致,从而整体形成翘曲。通过关键字*LOAD_THERMAL_LOAD_CURVE对上面两个板层施加温度载荷,且温度场随着时间变化而变化。0~100ms,第 一层4个角在z方向固定约束;100~120ms释放边界条件,让上部(第1层和第2层)自由移动。在0~100毫秒之间,进行单向耦合仿真,16个焊球的变形会受到边界位移的影响,但PCB结构的翘曲变形不会受到焊球反作用力的影响(表面张力、附着力和压力)。而在100~120毫秒之间实行双向耦合:既会将界面的边界位移施加给焊球,同时也会将反作用力(表面张力、附着力和压力)反馈给结构,从而考虑焊球表面张力对PCB结构的反作用力的影响,动画中可以看到焊球的变形更加平滑。
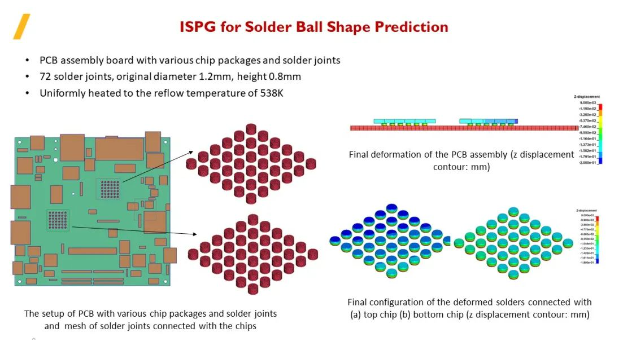
ISPG用于焊球形状预测。左图为一个包含不同芯片封装PCB板模型,芯片和电路板之间用焊球连接。两块区域包含72个焊球,每个焊球原始直径1.2mm,高度0.8mm。将整个模型均匀回流加热至538K,观察回流焊过程中焊球的变形。右上图为PCB组件结果变形(z位移轮廓:mm);右下图为(a)顶部芯片(b)底部芯片(z位移轮廓:mm)连接变形焊料的结果形态。
点击图片即可跳转原文观看视频
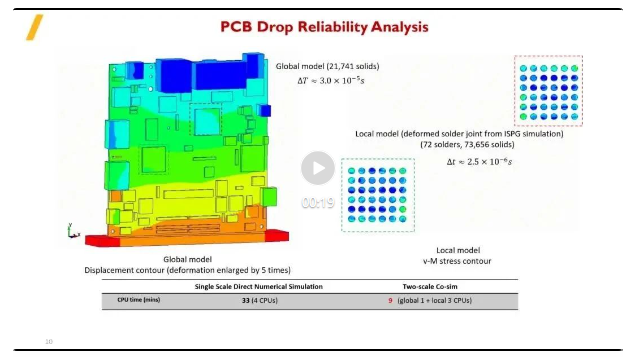
PCB跌落可靠性分析,将焊球结果的变形形态,导入整体电路板跌落模型中,通过对比单尺度直接数值模拟与双重尺度联合仿真,研究焊球在跌落过程中对整体部件的影响。
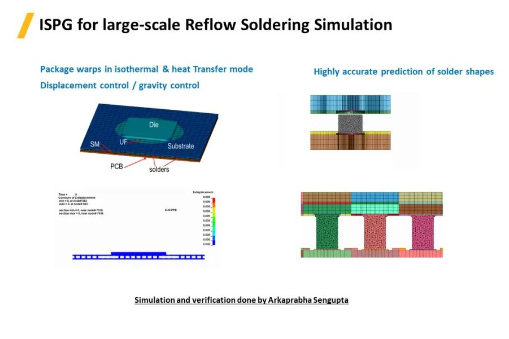
ISPG应用于大规模回流焊模拟过程。封装过程中PCB板常常会发生翘曲,焊球在重力载荷和边界位移条件的作用下发生变形,实验表明模拟过程ISPG方法精准的预测到了每个焊球的变形。

利用ISPG进行简化封装模型的焊接组装过程仿真,封装和PCB用简化的方块表示,模拟过程包含三个步骤:将模具基质加热到205℃,然后进行焊接,然后冷却到150℃。100个焊点的模型(包含15.2万个节点)采用10个CPU计算,运行时间为2.5小时;若采用64个CPU运算1,225个焊点(包含102万个节点)的类似模型,则仅耗时7.6小时,在确保精度的前提下,计算效率非常高。
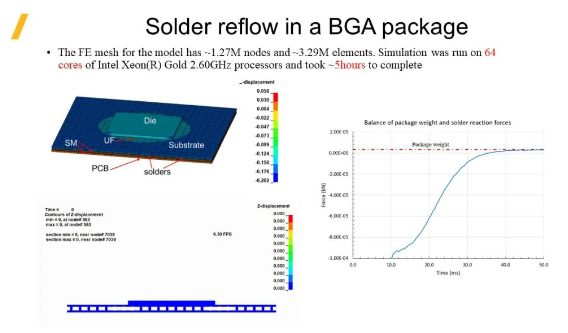
BGA封装中的回流焊,模型相对更复杂,其包含有限元网格节点数约为127万,单元数约为329万。在64核Intel Xeon(R) Gold 2.60GHz CPU上运行计算,耗时约5小时。右侧图表可以看到在该模型变形过程中,焊球顶端对上板的作用力趋于某个平衡点的过程,并且这个作用力与上板的重量一致。从这点也可以证明,ISPG方法的精度之高。
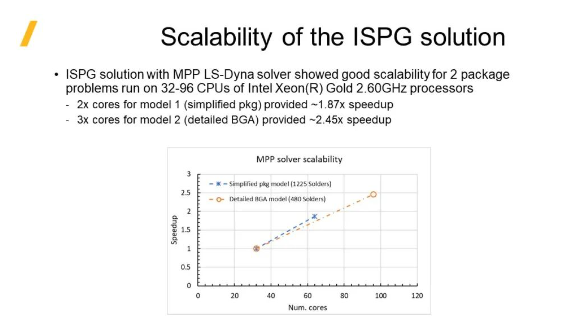
ISPG方法良好的可扩展性。在Intel Xeon(R) Gold 2.60GHz CPU的32-96个CPU上计算, 采用LS-DYNA MPP版本的ISPG方法显示出良好的可扩展性:

10,000个回流焊模拟的效率测试,模型采用10,000个焊球总共包含17,187,605个节点和32,303,312个单元,160个CPU运行时间为91小时;320 个CPU运行时间为55小时,比采用160 CPU快1.7倍,并行加速的可扩展性非常好。

当计算中需要模拟的物理几何形状及边界条件非常复杂时(比如尖角等),若没有网格更新,尖角的地方很难完全贴合,可能存在间隙及穿透现象。在焊球的桥接过程中,也需要网格不断地更新。因此,我们需要网格自动更新的自适应ISPG方法。
1)、使流体与固体面完全对齐,解决穿透问题
2)、根据结构面段特征自动调整颗粒分布,显著减少达到理想精度所需的节点数(用于压缩成型和粘合剂流动)
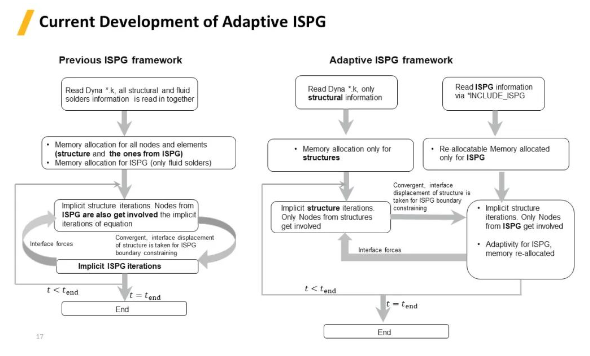
总体来说,原来的ISPG工作流程是将流体与固体的模型放在同一个文件里,并使用同一个迭代算法隐式求解,流固耦合计算中将固体表面作为边界,然后通过流体对固体的作用力反馈到固体表面。而自适应ISPG方法中流体跟固体模型完全分开,流体模型通过*INCLUDE_ISPG读取,并在内部形成独立的求解过程,流固耦合计算时,通过不同的点之间相互作用力以及位移来各自求解,也正是由于各自的独立运行,子循环更加容易。
点击图片即可跳转原文观看视频
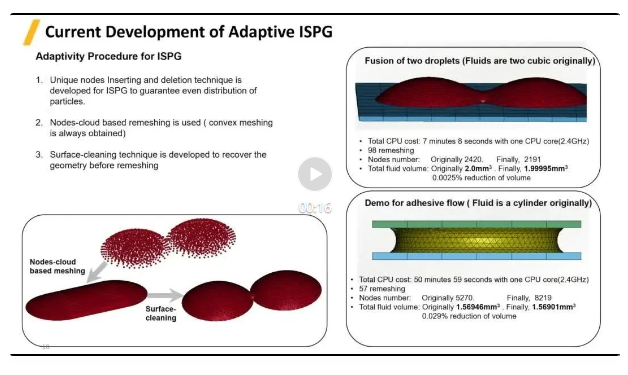
ISPG自适应过程
ISPG特有的节点插入和删除的技术可以保证重划分后粒子的均匀分布
使用基于节点云的网格重划分(始终得到凸面形状的网格)
利用表面清理技术在网格重画划分后恢复原来的几何形状
右上角案例展示了两个液滴的融合过程(流体原本是两个立方的),该案例使用一个CPU(2.4GHz)计算时间7分8秒,包含了98个网格更新过程,节点数从一开始的2,420个到后面的2,191个,总流体体积从2.0 mm3减少到1.99995 mm3,减小约0.0025%。证明网格更新的体积保持的效果相当理想。
右下角案例展示了粘性流体受两个板挤压,而沿着两个板之间扩张并结果溢出的过程。挤压过程使得粘性流体产生大变形成为薄薄的一层,该案例使用1个CPU (2.4GHz) 计算时间为50分钟59秒,包含了57个网格更新过程,节点数从一开始的5,270个到后面的8,219个,总流体体积从1.56946 mm3减少到1.56901 mm3,体积减小0.029%,体积保持效果同样表现优秀。
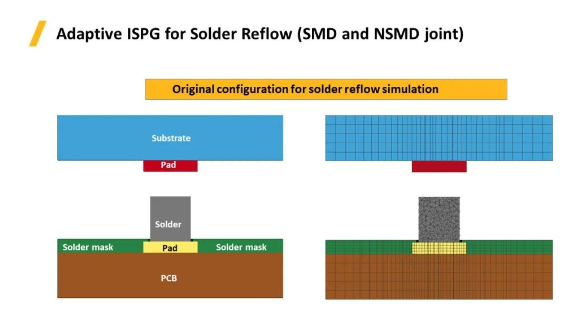
自适应ISPG网格更新算法应用于回流焊 (SMD和NSMD)模拟的过程,案例中展示的两个模型包含基板,焊盘,焊球,电路板和阻焊层等。
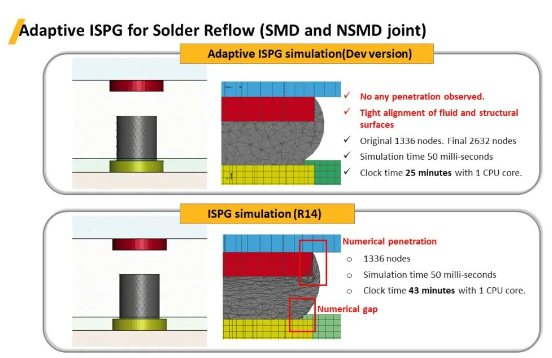
在新开发版本求解器(Dev版本),借助自适应ISPG的网格更新功能,焊球与结构边界完全贴合,没有出现任何穿透现象;且流体和固体表面紧密对齐;节点从原来的1,336个变化为2,632个,模拟时间50毫秒,1个CPU计算时间25分钟。
而原来的R14版本中,使用没有网格重划分功能的ISPG,焊球在变形过程中,在结构尖角处出现了间隙和穿透的现象,该过程模拟时间50毫秒,1,336个节点,1个CPU计算时间约为43分钟。
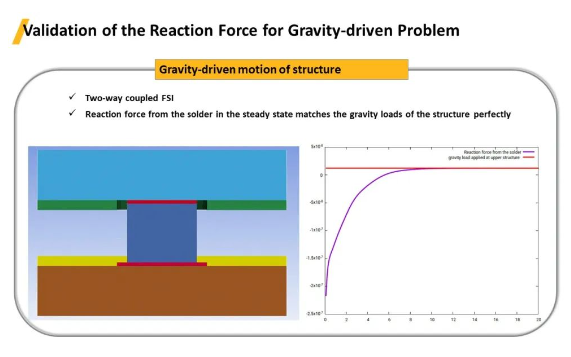
重力驱动问题反作用力的验证。重力驱动的结构运动为双向耦合FSI,将流固耦合过程中流体反馈给固体边界的作用力读取出来(右图图表),该作用力会稳定趋于一个数值平衡点,稳定状态下焊球的反作用力与结构的重力载荷完全吻合。
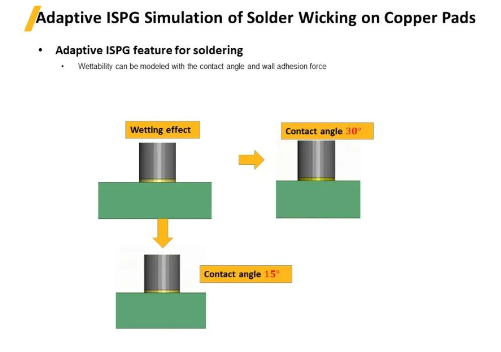
自适应ISPG模拟铜焊盘爬锡过程。润湿性可以用接触角和壁面附着力来建模。图中展示了定了不同接触角的吸锡过程模拟案例。接触角15°的模型,其润湿性明显比接触角30°的模型更好。
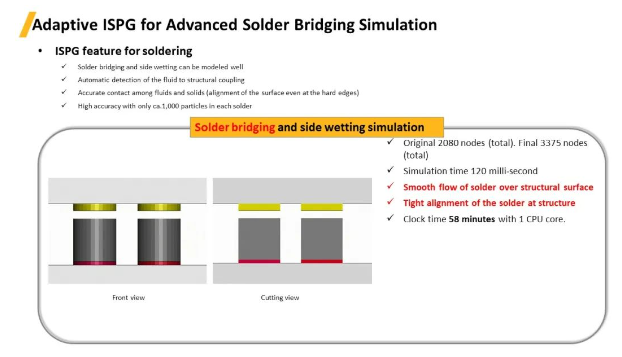
上图案例中展示了焊球桥接过程的模拟,当算法检测到当两个焊球的间隙足够近时,将其融合成一个焊球。
初始节点总数2,080个,结果变为3,375个
模拟时间120毫秒
焊球在结构表面的平滑流动
焊球在结构上的紧密贴合
1个CPU计算时间58分钟
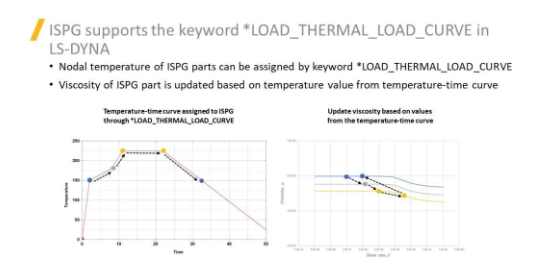
LS-DYNA ISPG方法支持*LOAD_THERMAL_LOAD_CURVE关键字,通过该关键字指定部件的节点温度,在模拟回流焊过程中施加持续的温度载荷(随着时间变化)。同时,可将ISPG部件的粘度定义为温度的函数,根据温度-时间曲线的温度值更新流体的粘度。
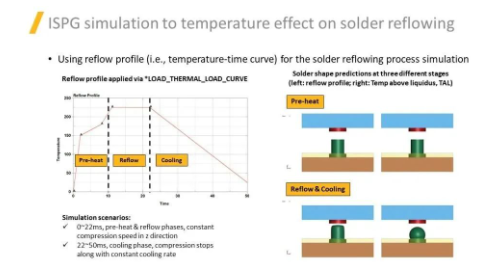
ISPG模拟温度对回流焊的影响,使用回流曲线定义过程中温度随时间的变化。模拟场景:
背景:胶粘剂在铝、碳纤维、钢等不同材料零部件的连接中的作用越来越大。
胶粘剂的表面张力、表面吸附力以及非牛顿流体特性对胶粘剂的流动至关重要。目前ISPG研发的内容包括非牛顿流体模型,考虑流体性质随时间和温度变化的效应,如流凝性流体、触变性流体、Bingham流体以及 Hershel-bulkley流体等。

目前ISPG支持三种流体粘度定义选项:
ISPG支持LS-DYNA中*LOAD_THERMAL_LOAD_CURVE关键字对ISPG部件进行节点温度分配。

上图展示了使用ISPG进行薄膜涂层的分析案例,图中使用了轴对称的模型。涂层粘性流体初始高度0.1毫米,半径0.5毫米,设置接触角为0.1度。可以看到,由于接触角非常的小,流体在表面吸附力作用下表面扩张成薄薄的一层,结果厚度0.00337毫米,半径是3.85毫米,厚度与半径之比非常小。模拟值与理论值误差小于0.2%,由此可以说明ISPG模拟精度非常高。
ISPG可以用非常粗的网格(原来是z方向的一层单元)精确地预测受微小接触角(甚至0.1°)影响的流体分布,在薄膜涂层模拟中具有很好的应用前景。
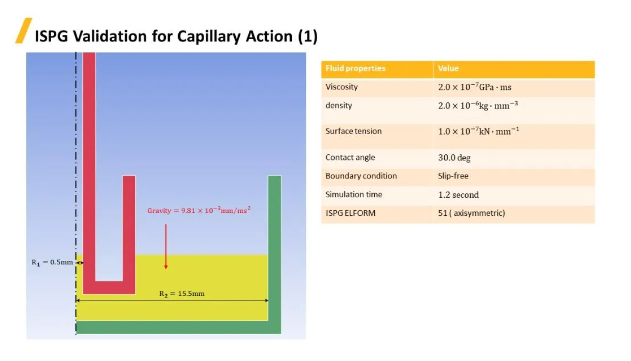
ISPG进行毛细管的仿真,这同样是一个轴对称的模型。内外两个容器,内容器半径0.5毫米,外容器半径15.5毫米,液体在细管状物体内侧,在表面张力和壁面吸附力的作用下,液体沿着壁面上升,结果整体形成凹面的形状。

将仿真得到的极高点压力和液体高度与理论值做比较,误差均在1%以内,精度表现十分理想。
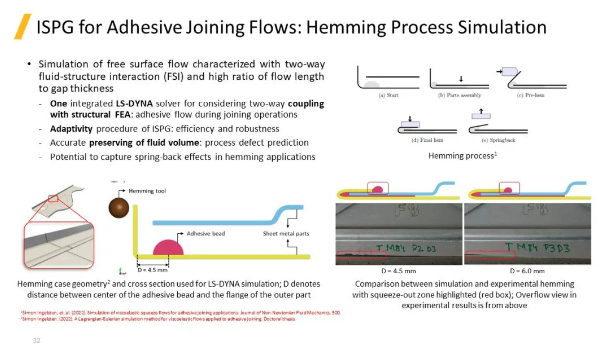
上图是使用ISPG模拟包边工艺过程中的粘胶剂流动过程的案例。这是一个自由表面流动问题,需要考虑双向流固耦合,同时流动长度与间隙厚度比例较高。
ISPG求解具有以下特点:
上图可以看到,中间粘胶上下各有一块金属板材,金属板材往下移动推动粘胶沿着板材表面延展扩张并结果溢出,粘胶厚度逐渐变薄。左图展示了包变的几何形状和LS-DYNA模型截面示意图,D为粘胶中心到包边距离。右侧展示了仿真与实验的结果对比,其中红框中为粘胶挤出的区域。下方为实验中粘胶实际溢出的结果。这里进行了两组实验和仿真,分别为D=4.5mm和D=6.5mm。可以看到D=6.5mm情况下粘性体扩展的更深,溢出更少,这与实验结果也是一致的。
点击图片即可跳转原文观看视频
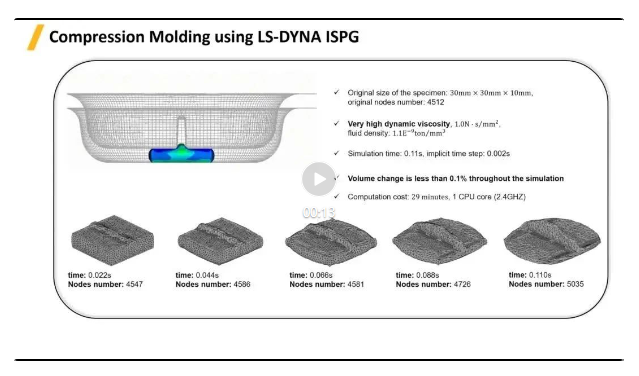
压塑成型过程,粘性流体在上下模挤压作用下沿空间扩张并成型。试件原始尺寸为30mm×30mm ×10mm,原始节点数4,512个,流体具有非常高的动态粘性度(1.0N?s)?m㎡ , 密度为(1.1E^(-9) ton)? mm3 ,仿真时间0.11s,隐式时间步长0.002s,使用1个CPU (2.4GHZ)计算时间29分钟,整个模拟过程中体积变化小于0.1%,且挤压过程中的流体边界保持的非常好。
点击图片即可跳转原文观看视频
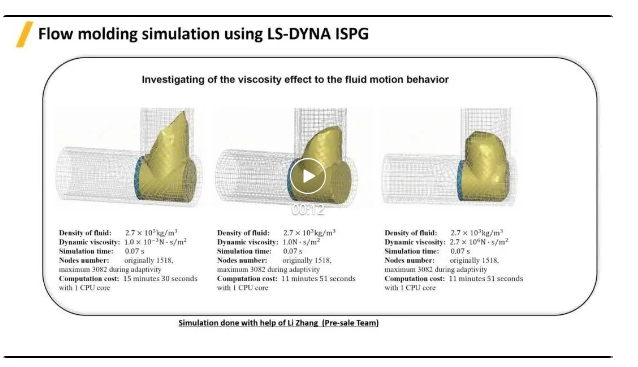
ISPG模拟流动模塑/成型过程,研究粘度对流体运动特性的影响。这里对比相同密度的粘性体在三种不同动态粘度下运动过程,仿真过程与实验非常接近。
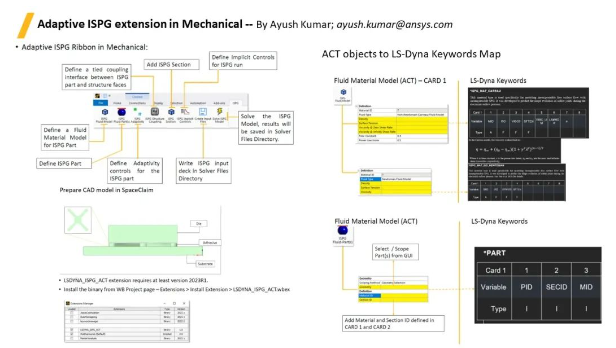

Mechanical界面中开发了用于ISPG分析的扩展插件,将来用户可以非常方便地在Mechanical界面下利用ACT进行ISPG前后处理。

ISPG是一种模拟自由表面流体行为的粒子方法,可以很容易地与结构有限元分析相结合,以准确有效地求解耦合相关的问题
ISPG能够准确有效地模拟具有表面张力和壁面粘附效应的自由表面流动
ISPG模型可以在ANSYS Mechanical界面中进行建模
实现了新的in core自适应框架,加快了网格自适应重划分地过程,并开发了基于节点云的ISPG自适应算法,具备更好的稳定性和可行性
开发了新的ISPG -结构耦合算法,使流体表面与结构表面对齐,解决了穿透问题。并根据结构面段信息自动调整粒子的分布,大大减少了了达到理想精度所需的节点数,提高了计算效率
开发了流体熔合算法,并利用该算法对焊料桥接进行了仿真。此外,还包含非牛顿流体模型,能够模拟非牛顿粘性流动问题
私信添加工作人员微信可获取相关模型及学习资料
更多内容分享,欢迎关注我们!
相关阅读
活动 | 使用LS-DYNA光滑粒子伽辽金(SPG)方法进行生物材料加工过程仿真
活动| Ansys LS-DYNA 2023R1&LS-DYNA Solver R14.0新功能介绍
活动 | LS-DYNA中自适应ISPG方法的新进展及其应用--回流焊、胶粘剂流动和涂层模拟
